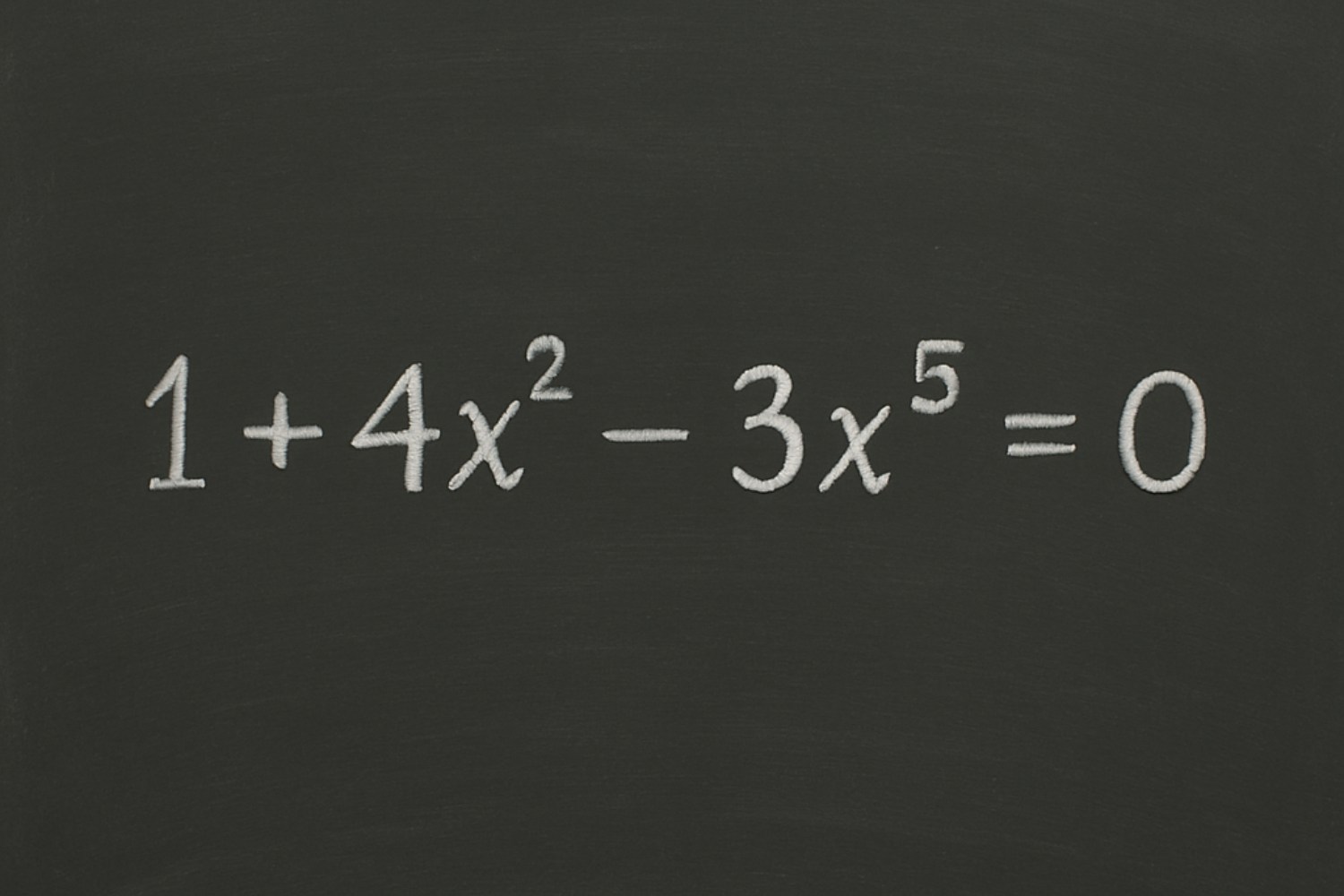Risolto uno dei problemi più antichi dell’algebra: le equazioni polinomiali di grado superiore (grazie alla successione di Catalan)

Scoperto un nuovo metodo per risolvere le equazioni polinomiali superiori grazie alla successione di Catalan: una vera e propria rivoluzione nell’algebra e nel calcolo computazionale

Immagine creata con IA

Uno dei nodi storici dell’algebra, finora ritenuto irrisolvibile in forma esatta, potrebbe finalmente essere stato sciolto. Il merito va al matematico Norman Wildberger, professore onorario presso la University of New South Wales di Sydney, che insieme all’informatico Dean Rubine ha proposto un nuovo metodo per affrontare le equazioni polinomiali superiori, pubblicato sulla rivista The American Mathematical Monthly.

Ma cosa significa tutto questo? Le equazioni polinomiali sono espressioni algebriche in cui una variabile è elevata a diverse potenze. Per esempio, un’equazione come 1 + 4x – 3x² = 0 è di secondo grado, mentre quelle di quinto grado o superiore, come 1 + 4x² – 3x⁵ = 0, rientrano nella categoria delle equazioni “superiori”.

Già dal XVI secolo, grazie agli studi dei matematici italiani, si conoscevano soluzioni esatte per le equazioni fino al quarto grado. Ma nel 1832, il genio francese Évariste Galois dimostrò che le equazioni di grado

Leggi tutto: https://www.greenme.it/scienza-e-tecnologia/risolto-equazioni-polinomiali-catalan/

LaCittaNews è un motore di ricerca di informazione in formato magazine, aggrega e rende fruibili, tramite le sue tecnologie di ricerca, in maniera  automatica, gli articoli più interessanti presenti in Rete.  LaCittaNews non si avvale di nessuna redazione editoriale.   =>  DISCLAIMER